- Source code is available on GitHub Github Neural Architecture
- Environments: Python 3.10, PyTorch 2.1.1
- To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.
Reusable neural blocks
Complex deep learning models have large stack of neural transformation such as convolution, fully connected network layers, activations, regularization modules, loss functions or embedding layers.
Creating these models using basic components from existing deep learning library is a daunting task. A neural block aggregates multiple components of a neural network into a logical, clearly defined function or task. A block is a transformation in the data flow used in training and inference.
Neural blocks in PyTorch
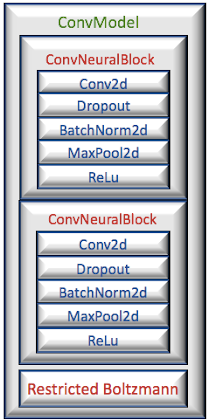
Modular convolutional neural network
- Conv2d: Convolutional layer with input, output channels, kernel, stride and padding
- Dropout: Drop-out regularization layer
- BatchNorm2d: Batch normalization module
- MaxPool2d Pooling layer
- ReLu, Sigmoid, ... Activation functions
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 | class ConvNeuralBlock(nn.Module):
def __init__(self,
in_channels: int,
out_channels: int,
kernel_size: int,
stride: int,
padding: int,
batch_norm: bool,
max_pooling_kernel: int,
activation: nn.Module,
bias: bool,
is_spectral: bool = False):
super(ConvNeuralBlock, self).__init__()
# Assertions are omitted
# 1- initialize the input and output channels
self.in_channels = in_channels
self.out_channels = out_channels
self.is_spectral = is_spectral
modules = []
# 2- create a 2 dimension convolution layer
conv_module = nn.Conv2d(
self.in_channels,
self.out_channels,
kernel_size=kernel_size,
stride=stride,
padding=padding,
bias=bias)
# 6- if this is a spectral norm block
if self.is_spectral:
conv_module = nn.utils.spectral_norm(conv_module)
modules.append(conv_module)
# 3- Batch normalization
if batch_norm:
modules.append(nn.BatchNorm2d(self.out_channels))
# 4- Activation function
if activation is not None:
modules.append(activation)
# 5- Pooling module
if max_pooling_kernel > 0:
modules.append(nn.MaxPool2d(max_pooling_kernel))
self.modules = tuple(modules)
|
into a full fledge convolutional model, in the following build method.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | class ConvModel(NeuralModel):
def __init__(self,
model_id: str,
# 1 Number of input and output unites
input_size: int,
output_size: int,
# 2- PyTorch convolutional modules
conv_model: nn.Sequential,
dff_model_input_size: int = -1,
# 3- PyTorch fully connected
dff_model: nn.Sequential = None):
super(ConvModel, self).__init__(model_id)
self.input_size = input_size
self.output_size = output_size
self.conv_model = conv_model
self.dff_model_input_size = dff_model_input_size
self.dff_model = dff_model
@classmethod
def build(cls,
model_id: str,
conv_neural_blocks: list,
dff_neural_blocks: list) -> NeuralModel:
# 4- Initialize the input and output size
# for the convolutional layer
input_size = conv_neural_blocks[0].in_channels
output_size = conv_neural_blocks[len(conv_neural_blocks) - 1].out_channels
# 5- Generate the model from the sequence
# of conv. neural blocks
conv_modules = [conv_module for conv_block in conv_neural_blocks
for conv_module in conv_block.modules]
conv_model = nn.Sequential(*conv_modules)
# 6- If a fully connected RBM is included in the model ..
if dff_neural_blocks is not None and not is_vae:
dff_modules = [dff_module for dff_block in dff_neural_blocks
for dff_module in dff_block.modules]
dff_model_input_size = dff_neural_blocks[0].output_size
dff_model = nn.Sequential(*tuple(dff_modules))
else:
dff_model_input_size = -1
dff_model = None
return cls(
model_id,
conv_dimension,
input_size,
output_size,
conv_model,
dff_model_input_size,
dff_model)
|
The default constructor (1) initializes the number of input/output channels, the PyTorch modules for the convolutional layers (2) and the fully connected layers (3).
The class method, build, instantiates the convolutional model from several convolutional neural blocks and one feed forward neural block. It initializes the size of input and output layers from the first and last neural blocks (4), generate the PyTorch convolutional modules (5) and fully-connected layers' modules (6) from the neural blocks.
Modular variational auto-encoder
Finally, the variational auto-encoder, VAE is assembled by stacking the convolutional, variational and de-convolutional neural blocks.
Neural blocks in Deep Java Library
Deep Java Library (DJL) is an Apache open-source Java framework that supports the most commonly used deep learning frameworks; MXNet, PyTorch and TensorFlow. DJL ability to leverage any hardware configuration (CPU, GPU) and integrated with big data frameworks makes it and ideal solution for a highly performant distributed inference engine. DJL can be optionally used for training.
Everyone who has been involved with GPT-3 or GPT-4 decoder (ChatGPT) is aware of the complexity and interaction of neural components in transformers.
Let's apply DJL to build a BERT transformer encoder using neural blocks, knowing
- A BERT encoder is a stack of multiple transformer modules
- Pre-training block which contains BERT block, Masked Language Model (MLM) module and Next Sentence Predictor (NSP) with their associated loss functions
- A BERT block is composed of embedding block.
The following Scala code snippet illustrates the composition of a BERT pre-training block using the transformer encoder block, thisTransformerBlock, the Masked Language Model component, thisMlmBlock and the Next Sentence Prediction module, thisNspBlock.
class CustomPretrainingBlock protected (
mlmActivation: String
) extends AbstractBaseBlock {
lazy val activationFunc: java.util.function.Function[NDArray, NDArray] =
ActivationConfig.getNDActivationFunc(activationType)
// Transformer encoder block // 1- Initialize the shape of tensors for the encoder, MLM and NSP blocks lazy val thisTransformerBlock: BertBlock = BertBlock.builder().base()
.setTokenDictionarySize(Math.toIntExact(vocabularySize))
.build
// MLM block lazy val thisMlmBlock: BertMaskedLanguageModelBlock =
new BertMaskedLanguageModelBlock(bertBlock, activationFunc)
// NSP block lazy val thisNspBlock: BertNextSentenceBlock =
new BertNextSentenceBlock
// 1- Initialize the shape of tensors for the encoder, MLM and NSP blocks override def initializeChildBlocks(
ndManager: NDManager,
dataType: DataType,
shapes: Shape*): Unit
// 2- Forward execution (i.e. PyTorch forward / __call__ override protected def forwardInternal(
parameterStore: ParameterStore,
inputNDList: NDList,
training : Boolean,
params: PairList[String, java.lang.Object]): NDList
}
DJL provides developers with two important methods
- initializeChildBlock (1) initializes the shape of the tensors for the inner/child blocks
- forwardInternal (2) implement the forward execution of neural network for the transformer and downstream classifier.
def forwardInternal(
parameterStore: ParameterStore,
inputNDList: NDList,
training : Boolean,
params: PairList[String, java.lang.Object]): NDList = {
// Dimension batch_size x max_sentence_size
val tokenIds = inputNDList.get(0)
val typeIds = inputNDList.get(1)
val inputMasks = inputNDList.get(2)
// Dimension batch_size x num_masked_token
val maskedIndices = inputNDList.get(3)
val ndChildManager = NDManager.subManagerOf(tokenIds)
ndChildManager.tempAttachAll(inputNDList)
// Step 1: Process the transformer block for Bert
val bertBlockNDInput = new NDList(tokenIds, typeIds, inputMasks)
val ndBertResult = thisTransformerBlock.forward(
parameterStore,
bertBlockNDInput,
training)
// Step 2 Process the Next Sentence Predictor block
// Embedding sequence dimensions are // batch_size x max_sentence_size x embedding_size
val embeddedSequence = ndBertResult.get(0)
val pooledOutput = ndBertResult.get(1)
// Need to un-squeeze for batch size =1, // (embedding_vector) => (1, embedding_vector)
val unSqueezePooledOutput =
if(pooledOutput.getShape().dimension() == 1) {
val expanded = pooledOutput.expandDims(0)
ndChildManager.tempAttachAll(expanded)
expanded
}
else
pooledOutput
// We compute the NSP probabilities in case there are more than // a single sentence
val logNSPProbabilities: NDArray =
thisNspBlock.forward(
parameterStore,
new NDList(unSqueezePooledOutput),
training
).singletonOrThrow
// Step 3: Process the Masked Language Model block
// Embedding table dimension are vocabulary_size x Embeddings size
val embeddingTable = thisTransformerBlock
.getTokenEmbedding
.getValue(parameterStore, embeddedSequence.getDevice(), training)
// Dimension: (batch_size x maskSize) x Vocabulary_size
val logMLMProbabilities: NDArray = thisMlmBlock.forward(
parameterStore,
new NDList(embeddedSequence, maskedIndices, embeddingTable),
training
).singletonOrThrow
// Finally build the output
val ndOutput = new NDList(logNSPProbabilities, logMLMProbabilities)
ndChildManager.ret(ndOutput)
Thank you for reading this article. For more information ...
References
- PyTorch
- Deep Java Library
- Automating the configuration of a GAN in PyTorch
- github.com/patnicolas
- Environments: Python 3.8, PyTorch 1.8.1, Scala 2.12.15, Java 11, Deep Java Library 0.20.0
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning" Packt Publishing ISBN 978-1-78712-238-3