Target audience: Beginner
Estimated reading time: 5'
Physics-Informed Neural Networks (PINNs) are gaining popularity for integrating physical laws into deep learning models. Essential tools like vector operators, including the gradient, divergence, curl, and Laplacian, are crucial in applying these constraints.
Table of contents
What you will learn: How to implement the vector gradient, divergence, curl and laplacian operators in Python using SymPy library.
Notes:
- Environments: Python 3.10.10, SymPy 1.12, Matplotlib 3.8.2
- This article assumes that the reader is familiar with differential and tensor calculus.
- Source code is available at github.com/patnicolas/Data_Exploration/diffgeometry
- To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.
Introduction
Geometric learning addresses the difficulties of limited data, high-dimensional spaces, and the need for independent representations in the development of sophisticated machine learning models.
Note: This article is the 5th installment in our series on Geometric Learning in Python following
- Geometric Learning in Python: Basics introduces differential geometry as an applied to machine learning and its basic components.
- Geometric Learning in Python: Manifolds describes manifold components such as tangent vectors, geodesics with implementation in Python for Hypersphere using the Geomstats library.
- Geometric Learning in Python: Intrinsic Representation Reviews the various coordinates system using extrinsic and intrinsic representation.
- Geometric Learning in Python: Vector and Covector fields describes vector and covector fields with Python implementation in 2 and 3-dimension spaces.
The following description of vector differential operators leverages some of concept defined in the previous articles in the Geometric Learning in Python series and SymPy library.
SymPy is a Python library dedicated to symbolic mathematics. Its implementation is as simple as possible to be comprehensible and easily extensible with support for differential and integral calculus, Matrix operations, algebraic and polynomial equations, differential geometry, probability distributions, 3D plotting. The source code is available at github.com/sympy/sympy.git
In tensor calculus, a vector operator is a type of differential operator:
- The gradient transforms a scalar field into a vector field.
- The divergence changes a vector field into a scalar field.
- The curl converts a vector field into another vector field.
- The laplacian takes a scalar field and yields another scalar field.
Gradient
Consider a scalar field f
We create a class, VectorOperators, that wraps the following operators: gradient, divergence, curl and laplacian. The constructor initializes the function as an expression for which the various operators are applied to.
class VectorOperators(object):
def __init__(self, expr: Expr): # Expression for the input function
self.expr = expr
def gradient(self) -> VectorZero:
from sympy.vector import gradient
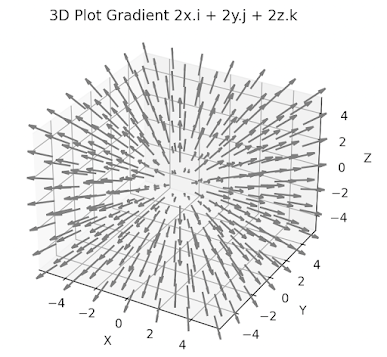
return gradient(self.expr, doit=True)Let's calculate the gradient vector for the function \[f(x,y,z)=x^{2}+y^{2}+z^{2} \] , as depicted in the plot below.
Fig. 1 3D visualization of function f(x,y,z) = x**2 + y**2 + z**2
The Python for the visualization of the function is described in Appendix (Visualization function)
The following code snippet computes the gradient of this function as \[\triangledown f(x,y,z) = 2x.\vec{i} + 2y.\vec{j} + 2y.\vec{k}\]
r = CoordSys3D('r')f = r.x*r.x+r.y*r.y+r.z*r.zvector_operator = VectorOperators(f) grad_f = vector_operator.gradient() # 2*r.x + 2*r.y+ 2*r.z
The function f is defined using the default Euclidean coordinates r. The gradient is depicted in the following plot implemented using Matplotlib module. The actual implementation is described in Appendix (Visualization gradient)
Fig. 2 3D visualization of grad_f(x,y,z) = 2x.i + 2y.j + 2z.k
Divergence
Divergence is a vector operator used to quantify the strength of a vector field's source or sink at a specific point, producing a signed scalar value. When applied to a vector F, comprising components X, Y, and Z, the divergence operator consistently yields a scalar result [ref 2]. \[div(F)=\triangledown .F=\frac{\partial X}{\partial x}+\frac{\partial Y}{\partial y}+\frac{\partial Z}{\partial z}\]
Let's implement the computation of the divergence as method of the class VectorOperators:
def divergence(self, base_vec: Expr) -> VectorZero:
from sympy.vector import divergence
div_vec = self.expr*base_vec
return divergence(div_vec, doit=True)Using the same instance vector_operators as with the gradient calculation:
divergence = vector_operators.divergence(r.i + r.j + r.k)
The execution of the code above produces the following:\[div(f(x,y,z)[\vec{i} + \vec{j}+ \vec{k}]) = 2x(y+z+xy)\]
Curl
In mathematics, the curl operator represents the minute rotational movement of a vector in three-dimensional space. This rotation's direction follows the right-hand rule (aligned with the axis of rotation), while its magnitude is defined by the extent of the rotation [ref 2]. Within a 3D Cartesian system, for a three-dimensional vector F, the curl operator is defined as follows: \[ \triangledown * \mathbf{F}=\left (\frac{\partial F_{z}}{\partial y}- \frac{\partial F_{y}}{\partial z} \right ).\vec{i} + \left (\frac{\partial F_{x}}{\partial z}- \frac{\partial F_{z}}{\partial x} \right ).\vec{j} + \left (\frac{\partial F_{y}}{\partial x}- \frac{\partial F_{x}}{\partial y} \right ).\vec{k} \]. Let's add the curl method to our class VectorOperator as follow:
def curl(self, base_vectors: Expr) -> VectorZero:
from sympy.vector import curl
curl_vec = self.expr*base_vectors
return curl(curl_vec, doit=True)
For the sake of simplicity let's compute the curl along the two base vectors j and k:
curl_f = vector_operator.curl(r.j+r.k) # j and k direction only
The execution of the curl method outputs: \[curl(f(x,y,z)[\vec{j} + \vec{k}]) = x^{2}\left ( z-y \right).\vec{i}-2xyz.\vec{j}+2xyz.\vec{k}\]
Laplacian
In mathematics, the Laplacian, or Laplace operator, is a differential operator derived from the divergence of the gradient of a scalar function in Euclidean space [ref 3]. The Laplacian is utilized in various fields, including calculating gravitational potentials, solving heat and wave equations, and processing images.
It is a second-order differential operator in n-dimensional Euclidean space and is defined as follows: \[\triangle f= \triangledown ^{2}f=\sum_{i=1}^{n}\frac{\partial^2 f}{\partial x_{i}^2}\]. The implementation of the method laplacian reflects the operator is the divergence (step 2) of the gradient (Step 1)
def laplacian(self) -> VectorZero:
from sympy.vector import divergence, gradient
# Step 1 Compute the Gradient vector
grad_f = self.gradient()
# Step 2 Apply the divergence to the gradient
return divergence(grad_f)
Once again we leverage the 3D coordinate system defined in SymPy to specify the two functions for which the laplacian has to be evaluated
r = CoordSys3D('r')
f = r.x*r.x + r.y*r.y + r.z*r.z
vector_operators = VectorOperators(f)
laplace_op = vector_operators.laplacian()
print(laplace_op) # 6
f = r.x*r.x*r.y*r.y*r.z*r.z
vector_operators = VectorOperators(f)
laplace_op = vector_operators.laplacian()
print(laplace_op) # 2*r.x**2*r.y**2 + 2*r.x**2*r.z**2 + 2*r.y**2*r.z**2
Outputs: \[\triangle (x^{2} + y^{2}+z^{2}) = 6\] \[\triangle (x^{2}y^{2}z^{2})=2(x^{2}y^2 +x^{2}z^{2}+y^{2}z^{2}) \]
References
-------------
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3
Appendix
Visualization function
The implementation relies on
- Numpy meshgrid to setup the axis and values for the x, y and z axes.
- Matplotlib scatter method to display the values generated by the function f
The function to plot takes x, y and z grid values and to generate data f(x,y,z)
@staticmethod
def show_3D_function(f: Callable[[float, float, float], float], grid_values: np.array) -> NoReturn:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
# Setup the grid with the appropriate units and boundary
x, y, z = np.meshgrid(grid_values, grid_values, grid_values)
# Apply the function f
data = f(x, y, z)
# Set up plot (labels, legend,..)
ax: Axes = self.__setup_3D_plot('3D Plot f(x,y,z) = x^2 + y^2 + z^2')
# Display the data along x, y and z using scatter plot
ax.scatter(x, y, z, c=data)
plt.show()
Visualization gradient
The 3 components of the gradient vector as passed as argument, grad_f.
The implementation relies on
- Numpy meshgrid to setup the axis and values for the x, y and z axes.
- Matplotlib quiver method to display the gradient vectors at each grid values
@staticmethod
def show_3D_gradient(grad_f: List[Callable[[float], float]], grid_values: np.array) -> NoReturn:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
# Setup the grid with the appropriate units and boundary
x, y, z = np.meshgrid(grid_values, grid_values, grid_values)
ax = self.__setup_3D_plot('3D Plot Gradient 2x.i + 2y.j + 2z.k')
# Extract the gradient df/dx, df/dy and df/dz
X = grad_f[0](x)
Y = grad_f[1](y)
Z = grad_f[2](z)
# Display the gradient vectors as vector fields
ax.quiver(x, y, z, X, Y, Z, length=1.5, color='grey', normalize=True)
plt.show()
