Target audience: Intermediate
Estimated reading time: 5'
Struggling with the complex task of configuring your Apache Spark application?
Consider the innovative approach of a genetic algorithm, a search heuristic inspired by Charles Darwin's theory of evolution [ref 1]. This method applies the concepts of natural selection to efficiently determine the best configuration for your Apache Spark application. It aims to achieve an ideal balance between minimizing production costs and maximizing customer satisfaction.
What you will learn: How to apply genetic algorithm to optimize the configuration parameters for deployment to production.
Notes:
- Source code available at GitHub - Patrick Nicolas - Genetic Algorithm github.com/patnicolas/streaming/scala/org/pipeline/ga
- To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.
- Environments: Apache Spark 3.3.1, Scala 2.13.4
Apache Spark configuration
The goal is to identify the best settings for Apache Spark [ref 2] configuration parameters that minimize deployment expenses while ensuring high-quality service, as indicated by reduced latency. This goal will be converted into a fitness function during the genetic algorithm's development.
Tunable parameters
We define an Apache Spark configuration parameter with the following attributes:
- key: Spark parameter identifier
- value: Default or initial value for the parameter
- isDynamic: Is this parameter tunable?
- paramType: Type of the parameter (Float, Int,)
- range: Range of valid values (any values if undefined)
The subsequent portion of the Apache Spark configuration file demonstrates the characteristics of different configuration parameters. This includes parameters that are not tunable (non-dynamic).
{
"sparkParameters": [
{
"key": "spark.io.compression.snappy.blockSize",
"value":"32k",
"isDynamic": false,
"paramType":"String"
"sparkParameters": [
{
"key": "spark.io.compression.snappy.blockSize",
"value":"32k",
"isDynamic": false,
"paramType":"String"
},
{
"key": "spark.KryoSerializer.unsafe",
"value":true,
"isDynamic": true,
"paramType":"Boolean"
},
{
"key": "spark.KryoSerializer.buffer.max",
"value":"64m",
"isDynamic": true,
"paramType":"Int",
{
"key": "spark.KryoSerializer.unsafe",
"value":true,
"isDynamic": true,
"paramType":"Boolean"
},
{
"key": "spark.KryoSerializer.buffer.max",
"value":"64m",
"isDynamic": true,
"paramType":"Int",
"range":["16","32", "64", "96", "128"]
},
{
"key": "spark.KryoSerializer.buffer",
"value":"64m",
"isDynamic": true,
"paramType":"Int",
{
"key": "spark.KryoSerializer.buffer",
"value":"64m",
"isDynamic": true,
"paramType":"Int",
"range":["16","32", "64", "96"]
},
{
"key": "spark.worker.cleanup.interval"
"value":900,
"isDynamic": false,
"paramType":"Int",
},
{
"key": "spark.worker.cleanup.interval"
"value":900,
"isDynamic": false,
"paramType":"Int",
"range":["300","600", "900", "1200"]
},
},
...
{
"key": "spark.shuffle.file.buffer",
"value":"32k",
"isDynamic": true,
"paramType":"Int",
"range":["16","32", "64", "128","256"]
},
{
"key": "spark.driver.memory",
"value":"6g",
"isDynamic": true,
"paramType":"Int",
{
"key": "spark.driver.memory",
"value":"6g",
"isDynamic": true,
"paramType":"Int",
"range":["2","4", "6", "8","10"]
},
{
"key": "spark.executor.driverOverheadFactor",
"value":0.1,
"isDynamic": true,
"paramType":"Float",
},
{
"key": "spark.executor.driverOverheadFactor",
"value":0.1,
"isDynamic": true,
"paramType":"Float",
"range":["0.05","0.1", "0.15", "0.2","0.25"]
},
{
"key": "spark.executor.memory",
"value":"4g",
"isDynamic": true,
"paramType":"Int",
},
{
"key": "spark.executor.memory",
"value":"4g",
"isDynamic": true,
"paramType":"Int",
"range":["2","3","4","5","6"]
},
{
"key": "spark.executor.memoryOverheadFactor",
"value":0.1,
"isDynamic": true,
"paramType":"Float",
},
{
"key": "spark.executor.memoryOverheadFactor",
"value":0.1,
"isDynamic": true,
"paramType":"Float",
"range":["0.05","0.1","0.15","0.2","0.25"]
},
{
"key": "spark.default.parallelism",
"value":8,
"isDynamic": true,
"paramType":"Int",
},
{
"key": "spark.default.parallelism",
"value":8,
"isDynamic": true,
"paramType":"Int",
"range":["4","8", "16", "24","32"]
},
},
...
]
}
Example of a Spark configuration parameters
The parameter spark.executor.memory is a dynamic, tunable integer variable with 2, 3, 4, 5, & 6g valid values.
The parameter spark.io.compression.snappy.blockSize is not tunable so the value 32k is immutable.
Fitness function
The fitness function is a balance between service delivery quality and the hourly deployment cost.
Our assumptions are as follows:
- The deployment cost per hour rises linearly with the number of servers or containers used, denoted by N.
- The adverse effect of latency on customer satisfaction and retention is estimated to grow exponentially with increasing latency L.
The fitness is consequently defined as... \[ fitness=\frac{1}{e^{\alpha L} + \beta N}\]
Genetic algorithm basics
Inspired by Charles Darwin's theory of natural evolution, a genetic algorithm is a search method that reflects the principles of natural selection. In this approach, the most suitable individuals are selected for reproduction to produce the next generation.
Scala's object-oriented and functional programming capabilities can be utilized to execute the computational process of an evolutionary algorithm.
Developed by John Holland in the 1970s [ref 2], Genetic Algorithms draw their characteristics from Darwin's evolution theory. A living organism is composed of cells, which contain identical chromosomes. These chromosomes, made up of DNA strings, act as a blueprint for the entire organism. A chromosome is made up of genes, which are DNA segments encoding specific proteins.
The first step in reproduction is recombination (or crossover), where genes from the parents form a completely new chromosome (offspring), which may then undergo mutation. During mutation, one or more elements, also known as individuals of the DNA strand or chromosome, are altered. These changes are primarily due to errors in copying genes from the parents. The organism's success in its environment determines its fitness.
In the field of computer science, Genetic Algorithms represent a problem-solving technique that emulates natural processes. They employ a combination of selection, recombination, and mutation to evolve a group of candidates for solving a particular problem. The fundamental computational steps are as follows:
- Initialize the population (search space) with a set of random chromosomes, each representing a specific Apache Spark configuration.
- Convert these chromosomes into a vector of real or integer values, or a string of bits.
- Pair chromosomes for crossover. This involves using a crossover rate to exchange a fragment or section of the "parent" chromosomes from a random point in the encoded string or vector.
- Mutate chromosomes by altering one or more of their elements (bits) using a randomly generated index, governed by a mutation rate.
- Evaluate each chromosome using a fitness function.
- Choose the most fit chromosomes (those that meet the minimum fitness criteria) for reproduction.
- Repeat the reproduction cycle (steps 2 to 6) for the newly formed population until a stop condition is reached.
Each genetic operator (selection, crossover, and mutation) depends on a specific parameter:
- The selection rate is a random threshold value used to reduce the current chromosome population based on their fitness.
- The crossover rate determines the index at which elements or bits of two parent chromosomes are swapped.
- The mutation rate calculates the index of the element(s) or bit(s) in a chromosome that undergo mutation (or flipping).
Implementation
The initial phase involves converting the configuration parameters into genetic components. Every parameter is represented as a gene, corresponding to the type of that parameter. For example, a parameter with an integer attribute is linked with an instance of Gene[Int].
Illustration of association configuration parameters and genetic components
A configuration represents a distinctive, tunable collection of Spark parameters, which the genetic algorithm treats and manages as a chromosome. The goal of the genetic algorithm is to identify the most suitable chromosome and its corresponding Spark configuration for the application, thereby optimizing the objective (or fitness).
Encoding
The first step is to implement the configuration and parameters as respective classes, SparkConfiguration and ParameterDefinition.
case class SparkConfiguration(sparkParameters: Seq[ParameterDefinition])
case class ParameterDefinition(
key: String,
value: String,
isDynamic: Boolean,
paramType: String,
range: Seq[String] = Seq.empty[String])
Next, we establish the genetic encoder responsible for transforming genes to and from configuration parameters [ref 4]. The GAEncoder trait encompasses two characteristics:
- encodingLength: The number of bits required to represent a parameter's value.
- range: A sequence of valid, adjustable values applicable to this parameter.
There are three primary methods:
- rand: This method initializes a parameter value randomly.
- apply: This function encodes a parameter's value into a sequence of bits.
- unapply: This procedure decodes a bit sequence back into a parameter value.
traitGAEncoder[T]{
val encodingLength: Int
val range: Seq[T]
def rand: T
def apply(t: T): BitsRepr
def unapply(bitsRepr: BitsRepr): T
}
Here's a genetic encoder for an Apache Spark configuration parameter of the Int type. The encoding function, 'apply', checks whether the parameter value, 't', falls within the valid range.
final class GAEncoderInt(
override val encodingLength: Int,
override val range: Seq[Int]) extends GAEncoder[Int]{
private[this] val encoder = new BitsIntEncoder(encodingLength)
override def rand: Int = Random.shuffle(range).head
@throws(classOf[GAException])
override def apply(t: Int): BitsRepr = {
if(!range.contains(t))
throw new GAException(s"Value $t violates constraint of quantizer")
encoder(t)
}
override def unapply(bitsRepr: BitsRepr): Int = encoder.unapply(bitsRepr)
}
Gene
A Gene serves as the genetic representation of a configuration parameter. Consequently, its constructor requires the following:
- The name of the parameter, referred to as 'id'.
- The value of the parameter denoted as 't'.
- An encoder, gaEncoder that corresponds to the parameter's type.
To minimize its memory usage and facilitate direct bit manipulation, the sequence of bits, 'bitsSequence', is transformed into a Java BitSet.
class Gene[T : Ordering] (id: String, t: T, gaEncoder: GAEncoder[T]) {
// Encoding as a sequence of {0, 1}
private[this] val bitsSequence: BitsRepr = gaEncoder(t)
// Encoding as Bit set
private[this] val encoded: util.BitSet = {
val bs = new java.util.BitSet(gaEncoder.encodingLength)
bitsSequence.indices.foreach(index => bs.set(index, bitsSequence(index) == 1))
bs
}
def mutate(mutationProb: Double): Gene[T] = {
(new MutationOp{
override val mutationProbThreshold: Double = mutationProb
}).mutate(this)
}
The method mutate invokes the mutation operator, MutationOp, described in the next section.
Chromosome
A chromosome symbolizes a Spark configuration. Assuming the configuration parameters are of two types (namely Float and Int), the constructor accepts two parameters:
- features1: This represents the features/genes of one type.
- features2: This encompasses the features/genes of the other type.
Additionally, the attribute 'fitness' accumulates the score for the specified set of configuration parameters.
class Chromosome[T : Ordering, U : Ordering](
features1: Seq[Gene[T]],
features2: Seq[Gene[U]]){
var fitness: Double = -1.0
def xOver(
otherChromosome: Chromosome[T, U],
xOverThreshold: Double ): (Chromosome[T, U], Chromosome[T, U]) =
(new XOverOp{
override val xOverProbThreshold: Double = xOverThreshold
}).xOver(this, otherChromosome)
def mutate(mutationProb: Double): Chromosome[T, U] = {
(new MutationOp{
override val mutationProbThreshold: Double = mutationProb
}).xOver(this)
}
}
The method 'xOver' executes the genetic crossover as outlined in the 'XOverOp' trait.
A crucial part of encoding a chromosome involves transforming a Spark configuration into a typed Chromosome, featuring integer and floating point parameters/genes.
A crucial part of encoding a chromosome involves transforming a Spark configuration into a typed Chromosome, featuring integer and floating point parameters/genes.
The process of encoding a Spark configuration is carried out by the 'encode' method. This involves purifying the parameter values from any units (denoted as 'cleansedParamValue'). The type of the configuration parameter, referred to as 'paramType', is utilized to create the encoder and gene of the suitable type.
def encode(sparkConfig: SparkConfiguration): Chromosome[Int, Float] = {
val floatGenes = ListBuffer[Gene[Float]]()
val intGenes = ListBuffer[Gene[Int]]()
sparkConfig.sparkParameters.foreach(paramValue => {
val value = paramValue.value
val cleansedParamValue: String =
if (!value.last.isDigit) value.substring(0, value.length - 1)
else value
paramValue.paramType match {
case "Int" =>
val encoder = new GAEncoderInt(encodingLength = 6, paramValue.range.map(_.toInt))
val intGene = Gene[Int](paramValue.key, cleansedParamValue.toInt, encoder)
intGenes.append(intGene)
....
The corresponding method decode is omitted in this post but is available on GitHub ConfigEncoderDecoder.scala
Mutation
The mutation process of a chromosome occurs in two stages:
- The genetic algorithm chooses a gene for mutation if the mutation probability falls below a specified threshold.
- A bit within the bit sequence is randomly selected and flipped based on a certain probability.
Illustration of mutation of a chromosome
It's important to note that mutating a bit sequence might not always result in a decoded value that is within the valid range set by the configuration parameter.
The 'MutationOp' trait encapsulates the implementation of the two-step mutation process. The first 'mutate' method applies the second mutation step to the chosen gene. Meanwhile, the second 'mutate' method carries out the first step of mutation on the chromosome.
trait MutationOp {
self =>
protected[this] val mutationProbThreshold: Double
private[this] val rand = new Random(42L)
// Mutation of a gene - Step 2
def mutate[T: Ordering](gene: Gene[T]): Gene[T] =
if(rand.nextDouble < mutationProbThreshold) {
val newValue = createValidMutation(gene, implicitly[Ordering[T]])
Gene[T](gene.getId, newValue, gene.getEncoder)
}
else
gene
def mutate[T: Ordering, U: Ordering](chromosomes: Seq[Chromosome[T,U]]): Seq[Chromosome[T,U]] = chromosomes.map(mutate(_))
// Mutation of a chromosome - Step 1
def mutate[T : Ordering, U: Ordering](chromosome: Chromosome[T, U]): Chromosome[TU]
The mutation operation initiates when a randomly generated value between [0, 1] remains below a specified low mutation rate, termed 'mutationProbThreshold'.
Afterward, the mutated bit sequence is decoded into a value of type T. This decoded value must fall within the range of valid values predetermined for this configuration parameter, a process known as 'createValidMutation'.
Regarding the mutation operator for a chromosome, it randomly selects one of the genes for mutation and then activates the mutation process with the chosen gene.
def mutate[T : Ordering, U: Ordering](chromosome: Chromosome[T, U]): Chromosome[T, U] =
if(rand.nextDouble < mutationProbThreshold) {
val features1 = chromosome.getFeatures1
val features2 = chromosome.getFeatures2
val chromosomeLength: Int = features1.length + features2.length
// Select the index of the gene to be mutated, randomly
val geneIndex = (chromosomeLength*Random.nextDouble).toInt
// If the index of the gene to mutate is within the first set of features or
// if there is only one set of features of same type..
if(geneIndex < features1.length || features2.isEmpty) {
val geneToMutate = features1(geneIndex)
val mutatedGene: Gene[T] = apply(geneToMutate)
features1.updated(geneIndex, mutatedGene)
}
// Otherwise the index of the gene to mutate is within the second set of features else {
val relativeIndex = geneIndex - features1.length
val geneToMutate: Gene[U] = features2(relativeIndex)
val mutatedGene: Gene[U] = apply(geneToMutate)
features2.updated(relativeIndex, mutatedGene)
}
Chromosome[T, U](features1, features2)
}
else
chromosome
Note: For the decoding of a bit sequence into an actual value, it's necessary to establish an implicit ordering for the types T and U associated with the parameters/genes.
Crossover
The crossover process involves dividing two 'parent' chromosomes and then merging their upper and lower segments to create two new 'offspring' chromosomes.
Illustration of cross-over
The crossover operator is exclusively applied to chromosomes.
Exploring the implementation of crossover between two chromosomes, we find the method 'xOver', which takes the two original chromosomes as its arguments.
def xover[T : Ordering, U : Ordering](
chromosome1: Chromosome[T, U],
chromosome2: Chromosome[T, U]
): (Chromosome[T, U], Chromosome[T, U]) = {
if(rand.nextDouble < xOverProbThreshold) {
val xOverIndex = (chromosome1.size()*Random.nextDouble).toInt
val features1Len = chromosome1.getFeatures1.length
// The cross-over cut-off is done within the first set of genes, preserving
// the second set of genes ..
if(xOverIndex < features1Len)
xOverFirstFeatures(chromosome1, chromosome2)
// Otherwise the cross-over is performed within the second set of genes
else
xOverSecondFeatures(chromosome1, chromosome2)
}
else
(chromosome1, chromosome2)
}
Several approaches exist for choosing candidate chromosomes for crossover [ref 5]. Three frequently used strategies include:
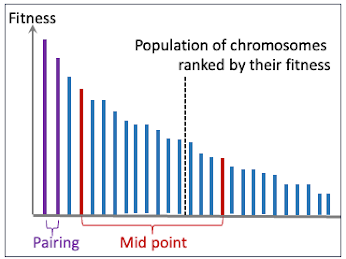
- midPoint: This method involves dividing the population of ranked chromosomes into two groups and then combining these groups.
- pairing: This strategy selects chromosome pairs that are contiguous in terms of their ranking.
- random: This approach randomly selects two candidate chromosomes.
The crossover strategy, xOverStrategy is applied to a population of chromosomes ranked in decreasing value of their fitness as illustrated in the code snipped below.
def xover[T : Ordering, U : Ordering](chromosomes: Seq[Chromosome[T, U]],xOverStrategy: String): Seq[Chromosome[T, U]] = xOverStrategy match {case "midPoint" =>val midPoint = chromosomes.length >> 1val (topChromosomes, botChromosomes) = chromosomes.splitAt(midPoint)val (offSprings1, offSpring2) = (0 until midPoint).map(index => xover(topChromosomes(index), botChromosomes(index))).unzipoffSprings1 ++ offSpring2case "pairing" =>val (offSprings1, offSpring2) = (chromosomes.indices by 2).map(index => xover(chromosomes(index), chromosomes(index+1))).unzipoffSprings1 ++ offSpring2.....}
Scoring
The 'ScoreOp' scoring operators calculate or update the fitness of a chromosome through the following steps:
- Decoding the chromosome into a valid Spark configuration.
- Initiating a SparkSubmit execution using the updated configuration.
- Determining the fitness of the chromosome.
trait ScoreOp{
self =>
protected[this] val execSparkSubmit: SparkConfiguration => (Int, Long)
protected[this] val latencyFactor: Float
protected[this] val serverHourlyCost: Float
def score(population: Seq[Chromosome[Int, Float]]): Seq[Chromosome[Int, Float]] =
population.map(score(_))
private def score(chromosome: Chromosome[Int, Float]): Chromosome[Int, Float] = {
val sparkConfig = ConfigEncoderDecoder.decode(chromosome) // Step 1
val (numServers, latency) = execSparkSubmit(sparkConfig) // Step 2chromosome.fitness = 1.0/(math.exp(latencyFactor*latency) + // Step 3
serverHourlyCost*numServers)
chromosome
}
The scoring operator allocates the execution of each configuration to various containers by simultaneously running Spark submit tasks concurrently.
Selection
The selection process is outlined in the 'SelectionOp' trait, which includes two methods:
- 'rand' - This method is used to initialize a population of chromosomes, up to a size of 'maxPopulationSize', with random values.
- 'select' - This method ranks chromosomes according to their fitness, in decreasing order.
trait SelectionOp{
self =>
protected[this] val maxPopulationSize: Int
def rand[T : Ordering, U : Ordering](
idsT: Seq[String],
gaEncoder1: GAEncoder[T],
idsU: Seq[String],
gaEncoder2: GAEncoder[U]
): Seq[Chromosome[T, U]] =
Seq.fill(maxPopulationSize)(Chromosome.rand(idsT, gaEncoder1, idsU, gaEncoder2))
def select[T : Ordering, U : Ordering](chromosomes: Seq[Chromosome[T, U]]): Seq[Chromosome[T, U]] =
chromosomes.sortWith(_.fitness > _.fitness).take(maxPopulationSize)
Mating cycle
A replication cycle involves the processes of crossing-over, mutation, scoring, and ultimately selecting chromosomes based on their fitness values. This cycle is encapsulated in the 'Reproduction' class, which has the following attributes:
- execSparkSubmit: A function for executing Spark Submit.
- latencyFactor: A factor used in calculating the fitness of chromosomes, based on latency.
- serverHourlyCost: The hourly cost of an average server or container, factored into the fitness calculation of chromosomes.
- maxPopulationSize: The upper limit on the number of chromosomes throughout the mating cycle.
- xOverProbThreshold: A threshold value determining the likelihood of initiating a crossover.
- mutationProbThreshold: A threshold value for the probability of triggering a mutation.
- xOverStrategy: The strategy employed for crossover.
- stopCondition: A function or condition that signals when to end the execution of the genetic algorithm.
class Reproduction protected (
val execSparkSubmit: SparkConfiguration => (Int, Long),
override val latencyFactor: Float,
override val serverHourlyCost: Float,
override val maxPopulationSize: Int,
override val xOverProbThreshold: Double,
override val mutationProbThreshold: Double,
xOverStrategy: String,
stopCondition: Seq[Chromosome[Int, Float]] => Boolean
) extends ScoreOp with SelectionOp with XOverOp with MutationOp {
def mate(
idsInt: Seq[String],
gaEncoderInt: Seq[GAEncoder[Int]],
idsFloat: Seq[String],
gaEncoderFloat: Seq[GAEncoder[Float]]): Seq[Chromosome[Int, Float]] = {
// Initialization of chromosomes
val initialChromosomes = Seq.fill(maxPopulationSize)(
Chromosome.rand(idsInt, gaEncoderInt, idsFloat, gaEncoderFloat)
)
// Recursive reproduction cycle
mate(initialChromosomes, iterationCount = 0)
}
@tailrec
private def mate(
chromosomes: Seq[Chromosome[Int, Float]],
iterationCount: Int): Seq[Chromosome[Int, Float]] = {
val offSprings = xOver(chromosomes, xOverStrategy)
val mutatedChromosomes = mutate(chromosomes ++ offSprings)
val scoredChromosomes = score(mutatedChromosomes)
val selectedChromosomes = select(scoredChromosomes)
// If condition met, exit
if (iterationCount > 16 || stopCondition(selectedChromosomes)) selectedChromosomes
// Otherwise recurse
else mate(selectedChromosomes, iterationCount + 1)
}
The 'mate' method executes the reproduction cycle, as outlined in the section detailing the basics of Genetic Algorithms. It requires the following inputs:
- idsInt: A list of identifiers for configuration parameters that are of type Int.
- gaEncoderInt: An encoder tailored for each configuration parameter of type Int.
- idsFloat: A series of identifiers for configuration parameters that are of type Float.
- gaEncoderFloat: An encoder specific to each of the configuration parameters of type Float.
This method is executed as tail recursion for enhanced efficiency, with a safety mechanism in the form of a stop condition based on the iteration count, set to 16. The flexible stop condition concludes the search by assessing the most recent group of chromosomes.
Examples of possible stop conditions include:
The scenario where the fittest chromosome (representing a Spark Configuration) exhibits a fitness level that is at least 20% higher than that of the next best chromosome.
val stopDiffCondition = (chromosomes: Seq[Chromosome[Int, Float]]) =>
if(chromosomes.size == 1) true
else
chromosomes.head.fitness/chromosomes(1).fitness >= 1.20
A second scenario where fitness for the best chromosome is at least 50% better that the average fitness of all chromosomes.
val stopAveCondition = (chromosomes: Seq[Chromosome[Int, Float]]) =>
if (chromosomes.size ==1) true
else {
val chromosomesAveFitness = chromosomes.map(_.fitness).sum/chromosomes.size
chromosomes.head.fitness / chromosomesAveFitness > 2.0
}Evaluation
The reproduction cycle applied to large set of parameters is very computationallyl intensive. Therefore, we restricted our test to 5 configuration parameters:
Integer parameters
spark.default.parallelism
spark.executor.memory
spark.driver.memory
Float parameters
spark.executor.memoryOverheadFactor
spark.executor.driverOverheadFactor
All other Spark configuration parameters are fixed.
We consider the ratio of fitness of the best chromosome over the average fitness of all chromosomes > 1.5 as stopping condition.
The fitness function is defined as \[ fitness=\frac{1}{e^{0.001L} + 0.47N}\]
where L is the latency in milliseconds and N the number of AWS EC2 m5d.2xlarge on-demand instances.
The test uses the Spark deployment for the storm tracking application described in Tracking storms with Kafka/Spark streaming [ref 6]
The maximum number of iterations is set to 24.
To ensure a viable and robust deployment of this Spark application in a production environment, a more extensive evaluation involving a greater number of parameters is necessary.
Alternative methods
Alternative methods can be inspired by the techniques used in tuning hyper-parameters of ML models [ref 7].
Gradient search: This technique estimates the derivative or gradient of the fitness function over the configuration parameters pj
\[p_{i}^{t+1} = p_{i}^{t} + \eta \frac{\partial fitness}{\partial p_{j}}\]
Reinforcement learning: In this approach, the fitness function is converted into a reward applied to any action on the configuration parameters. The values of the configuration parameters define the state of the reinforcement learning model.
Bayesian optimization: The Bayesian approach considers the optimization of the Spark configuration as a random entity and assigning a prior distribution to it. This prior reflects our assumptions about the function's behavior. Once we collect evaluations of the function, treated as data, this information is used to update the prior, resulting in the posterior distribution of the objective function. Subsequently, this posterior distribution is employed to create an acquisition function which is instrumental in determining the next point of query.
References
[2] Apache Spark
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3