Target audience: Beginner
Estimated reading time: 5'
Have you ever faced the need to rationalize the prediction made by one of your models, or to identify which features are crucial? If so, SHAP values and plots are your go-to resources, offering the fundamental structure for an explanation.
What you will learn: How to use SHAP values and plots to identify the most significant features for multi-classification models.
Notes:
- Environments: Python 3.10.10, Scikit-learn 1.3.2, Shap 0.43
- Comments, error checking and debugging statements are omitted in source code.
- Full source code is available on Github https://github.com/patnicolas/Data_Exploration/stats
Introduction
SHAP (SHapley Additive exPlanations), which is based on the concepts of game theory, is employed to clarify the predictions of machine learning models [ref 1]. This approach evaluates the contribution of each feature to a model's prediction, aiding in pinpointing the key features and understanding their specific effects on the model's results.
The complete description of the theory behind SHAP [ref 2] is beyond the scope of this article but can be summarized as follow:
For M players, S a subset of M players
\[\varphi _{i}= \sum _{S\sqsubseteq M-\left \{ i \right \} }\frac{|S|! (|M|-|S|-1)!}{|M|!}\left ( f(S \cup \left \{ i \right \}) -f(S)) \right )\] where f is the prediction model\[S\sqsubseteq M-\left \{ i \right \}\] is the subset S of players excluding player i
The prediction made by a model, denoted as , can be expressed as the total of its SHAP values plus a constant base value, as shown in the equation: .
To begin a global interpretation using SHAP, one should first look at the average absolute SHAP value for every feature across the entire dataset. This approach measures the average impact (whether positive or negative) of each feature's contribution to the predicted air quality index.
Use Case
SHAP values serve various purposes, including:
- Debugging models to spot biases or anomalies in the data.
- Assessing feature importance to pinpoint and eliminate features with minimal impact.
- Providing detailed explanations for individual predictions.
- Summarizing models using SHAP value summary plots.
- Detecting biases to determine if specific features have an undue influence on certain groups.
- Facilitating regulatory approval by elucidating the model's decision-making process.
In this article, our aim is to calculate SHAP values and analyze the significance of each feature in three classification models. These models are used to forecast Air Quality in 138 cities across the Philippines.
Dataset
We used the Air Quality Index (AQI) dataset of 138 Philippine cities weather data, available In Open Weather Map from Kaggle data repository [ref 3].
The 8 features are components that contribute to air pollution such as Carbon monoxide (CO), Nitrogen monoxide (NO), Nitrogen dioxide (NO2), Ozone (O3), Sulphur dioxide (SO2), Ammonia (NH3), and particulates (PM2.5 and PM10).
The 5 labels/classes are indexed as Good (1), Fair (2), Moderate (3), Poor (4), Very Poor (5).
SHAP values and plots
First we implement the class SHAPEval to compute the SHAP values and generate Summary, Dependency, Force and Decision plots, given a predictive model, model_prediction [ref 4].
class SHAPEval(object):
def __init__(self, model_predictor, plot_type: SHAPPlotType):
self.model_predictor = model_predictor
self.plot_type = plot_type
def __call__(self, validation_data: pd.array, column_names: List[AnyStr]) -> NoReturn:
# 1- Compute SHAP values
shap_descriptor = shap.KernelExplainer(self.model_predictor, validation_data)
shap_values = shap_descriptor.shap_values(validation_data)
# 2- Apply specific plot to validation data and extracted SHAP values
match self.plot_type:
case SHAPPlotType.SUMMARY_PLOT:
shap.summary_plot(shap_values, validation_data, feature_names=column_names)
case SHAPPlotType.PARTIAL_DEPENDENCY_PLOT:
shap.dependence_plot("o3", shap_values, validation_data, feature_names=column_names)
case SHAPPlotType.FORCE_PLOT:
data_point_rank = 8
shap.force_plot(
shap_descriptor.expected_value,
shap_values[data_point_rank,:],
validation_data[data_point_rank,:],
feature_names=column_names,
matplotlib=True)
case SHAPPlotType.DECISION_PLOT: shap.decision_plot( shap_descriptor.expected_value, shap_values, feature_names=column_names, link='logit') case _: raise Exception(f'Plot type {self.plot_type} is not supported')
The dunder special method, __call__ accepts a test dataset, validation_data, and a list of feature names, column_names, for the following purposes:
- To calculate SHAP values using a Kernel Explainer.
- To create various SHAP visualizations.
Different types of explainers exist for various models, such as the TreeExplainer for random forests, the SamplingExplainer for models with independent features, or the DeepExplainer for differentiable models [ref 5].
For our purposes, we have chosen the Kernel Explainer. Its approach of employing weighted linear regression to determine the significance of each feature is particularly well-suited for models like logistic regression, support vector machines, and neural networks.
Models
Following this, we use the SHAPEval method on each of the three models. The ModelEval class, designed for evaluating models, has a constructor with four parameters:
- filename: This refers to the location of the CSV file that holds the Air Quality Index data.
- dropped_features: A list of features deemed irrelevant, which will be omitted from the training dataset.
- label: The column that serves as the target for the classification model.
- val_train_split: This denotes the proportion of samples allocated for validation compared to training.
@dataclass
class TestMetric:
accuracy: float
f1: float
mean_squared_error: float
class ModelEval(object):
random_state = 5713
def __init__(self,
filename: AnyStr,
dropped_features: List[AnyStr],
label: AnyStr,
val_train_split: float):
def set_label(x: float) -> int:
return int(x) - 1
df = pd.read_csv(filename)
# Drop non features and label columns
dropped_features.append(label)
X = df.drop(dropped_features, axis=1)
# Apply standard normalization
X_scaled = StandardScaler().fit(X).transform(X)
# Select column containing label
y = df[label].apply(set_label)
# Train - validation split
self.feature_names = X.columns.values.tolist()
self.X_train, self.X_val, self.y_train, self.y_val = \
train_test_split(X_scaled, y, test_size=val_train_split, random_state=ModelEval.random_state)
def __call__(self, model_type: ModelType, plot_type: SHAPPlotType) -> TestMetric:
# Initialize the classification model
match model_type:
case ModelType.LOGISTIC_REGRESSION:
model = LogisticRegression( solver='lbfgs', max_iter=1000, penalty='l2', multi_class='multinomial')
case ModelType.SVM:
model = SVC( kernel="rbf", decision_function_shape='ovo', random_state=ModelEval.random_state)
case ModelType.MLP:
model = MLPClassifier(
hidden_layer_sizes=(32, 16),
max_iter=500,
alpha=0.0001,
solver='adam',
random_state=ModelEval.random_state)
case _:
raise Exception(f'Model name {model_type} is not supported')
# Train the model
model.fit(self.X_train, self.y_train)
# Compute SHAP values and selected plots
shap_eval = SHAPEval(model.predict, plot_type)
shap_eval(self.X_val, self.feature_names)
# prediction and quality metrics
y_predicted = model.predict(self.X_val)
return TestMetric(
accuracy_score(self.y_val, y_predicted),
f1_score(self.y_val, y_predicted, average='weighted'),
mean_squared_error(self.y_val, y_predicted)
)
The following code snippet instantiates the ModelEval class to generate a decision plot (SHAPPlotType.DECISION_PLOT) for the logistic regression (ModelType.LOGISTIC_REGRESSION)
test_filename = '../../data/Philippine_Air_Quality.csv'
test_drop_features = ['datetime', 'coord.lon', 'coord.lat', 'extraction_date_time', 'city_name']
test_label = 'main.aqi'
test_size = 0.01
try:
model_eval = ModelEval(test_filename, test_drop_features, test_label, test_size)
test_metrics = model_eval(ModelType.LOGISTIC_REGRESSION, SHAPPlotType.DECISION_PLOT)
except SHAPException as e:
print(str(e))
except Exception as e:
print(str(e))
Evaluation
The three models been evaluated are using Adam optimizer
- Logistic regression with L-BFGS solving and L2 regularization
- Support Vector Machine with Adam optimizer, radial basis function kernel function and ovo decision function shape
- Multi-layer perceptron with two hidden layers of respective sizes 32, 16 and Adam solver
Metrics
The quality metrics output for the three models are:
| Model | Accuracy | F1-Score | MSE |
| Logistic Regression | 0.928 | 0.924 | 0.119 |
| Support Vector Machine | 0.974 | 0.953 | 0.025 |
| Multi-Layer Perceptron | 0.992 | 0.989 | 0.002 |
Comparative summary plots
API: shap.summary_plot(shap_values, data, feature_names)
Initially, we calculate and present a summary report detailing the SHAP values for all three models: logistic regression, support vector machine, and multi-layer perceptron. This plot illustrates the positive and negative correlations between the predictors and the target variable.
The 'dotty' appearance of the plot arises from the inclusion of each data point from the training dataset.
By examining the distribution and positioning of the dots across various features, we can assess which features exert the most influence. Some features may demonstrate a uniform effect (indicated by closely grouped dots), whereas others may show more diverse impacts (evidenced by dots that are more widely scattered).
SHAP summary plot for Support Vector Machine with 96 samples
The data points in the plot are arranged along the X-axis based on their SHAP values, ranging from -0.6 to 2.2. The thickness of the stack at each SHAP value indicates how many data points have that particular value, representing the density or concentration of the SHAP value. Additionally, the vertical 'feature value' bar is colored to show the actual raw prediction values.
In these plots, the features like o3, pm2_5, and others are ordered from top to bottom according to their average absolute SHAP value.
The consistency of SHAP values across the three models—logistic regression, support vector machine, and multi-layer perceptron—emphasizes the significance of the o3 and pm2_5 components in influencing the predictions. Notably, the Multi-layer perceptron model displays one or two predominant SHAP values for each feature, aligning with its high f1 score as a classifier.
Dependency plot
API: shap.dependence_plot('o3', shap_values, data, feature_names)
The dependency plot illustrates the impact that one or two variables exert on the predicted result, revealing the nature of the relationship—whether it's linear, monotonic, or more intricate—between the target and the variables. This type of plot is especially useful for understanding models based on ensemble methods and deep learning.
We will proceed to create a SHAP dependence plot for the neural network model, utilizing a dataset of 780 samples.
SHAP dependency between o3 and pm10 components plot for MLP with 780 samples
The x-axis represents the numerical values of the feature o3. The y-axis shows the SHAP values for both o3 and pm10 features. The higher the value, the greater the impact on the prediction.
The high dispersion along the y-axis indicates that there is some dependency between the targeted feature o3 and other features, primarily pm10.
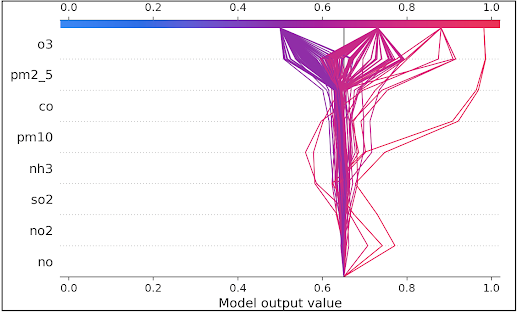
Decision plot
API: shap.decision_plot(expected_value, shap_values, feature_names, link='logit')
SHAP decision plots reveal the process by which complex models make their predictions, essentially illustrating the decision-making mechanism of these models. In these plots, features are ranked in order of their importance, which is calculated based on the observations being plotted.
Each observation's predicted outcome is depicted by a line of a specific color. These lines intersect the x-axis at the top of the plot, at points that correspond to the predicted values for the observations. The predicted value is what determines the color of the line, typically represented on a spectrum.
The plot effectively demonstrates how the contribution of each feature adds up to the final prediction made by the model.
The dataset's average prediction, also known as the base value, is set at 0.64. The features, such as o3 and others, are organized in a descending order based on their significance. Each line in the plot represents either a test or validation sample and shows the cumulative effect of each feature. A movement towards the right of the base value (0.64) signifies that the feature positively influences the prediction. Conversely, a shift towards the left indicates that the feature negatively affects the prediction.
In the plot, 156 validation samples are illustrated, culminating in four distinct final probability values: 0.43, 0.73, 0.88, and 0.98.
Force Plot
API: shap.force_plot(expected_value, shap_values[index,:], data[index,:], feature_names, matplotlib=True)
For each observation, you can create a sophisticated visualization known as the force plot. In these plots, features are arranged from left to right, with those making a positive impact positioned on the left and those with a negative impact on the right. For the 8th observation, the key features influencing the model's prediction are highlighted in red and blue. Red indicates the features that increased the model's score, while blue denotes the features that decreased the score.
SHAP observation force plot for 8th sample with logistic regression
Each feature's contribution is represented by an arrow, colored to reflect its impact. The size and orientation of these arrows demonstrate both the strength and the nature (positive indicated by red, negative by blue) of each feature's influence on the prediction.
As highlighted in the summary plot, the o3 component emerges as a primary feature, exerting a negative effect on the prediction with a score of -0.746. Conversely, the pm2_5 feature makes a positive contribution, impacting the prediction with a score of 0.246.
Limitations
Despite its usefulness, SHAP comes with certain constraints, including:
- It demands substantial computational resources, especially for intricate multi-label or multi-class models that use extensive datasets.
- The computation relies on the assumption of feature independence, particularly in the case of Kernel or Linear SHAP.
- While SHAP reveals the extent to which a feature influences a prediction, it does not explain how these features collectively contribute to the target variable.
Thank you for reading this article. For more information ...
References
----------------------------------
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning.
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning", Packt Publishing ISBN 978-1-78712-238-3