Friday, July 28, 2023

Compare Python, NumPy and PyTorch Performance

Target audience: Beginner
Estimated reading time: 4'

Recently, I embarked on a healthcare project that involved extracting diagnostic information from Electronic Health Records. While fine-tuning a BERT model, I noticed some atypical latency behaviors. This prompted me to conduct a performance comparison between Python lists, NumPy arrays, and PyTorch tensors.
The implementation relies on a timer decorator to collect latency values.


Table of contents
Follow me on LinkedIn

Notes: 
  • The implementation uses Python 3.11, Numpy 1.25.1, PyTorch 2.4
  • To enhance the readability of the algorithm implementations, we have omitted non-essential code elements like error checking, comments, exceptions, validation of class and method arguments, scoping qualifiers, and import statements.

Introduction

I assume that most readers are familiar with the various Python, NumPy and PyTorch containers used in this article. But just in case, here is a quick refresh:

Python list: A list in Python is similar to an array in C, C++, Java or Scala except that its elements can have different types.

Python arrays: Array is a container which can hold a fix number of items or elements. Contrary to lists, items of an array should be of the same type. Most of the data structures make use of arrays to implement their algorithms [ref 1].

NumPy arrays: A numPy array represents a multidimensional, homogeneous array of fixed-size items. It is implemented as a static buffer of contiguous values of identical types which index can be dynamically modified to generate matrix, tensor or higher dimension numerical structures [ref 2].

PyTorch tensors: Similarly to numpy arrays, PyTorch tensors are multi-dimensional arrays containing elements of a single data type. The tensors share the same semantic and operators as NumPy arrays but also support automatic differentiation and support GPU/Cuda math libraries [ref 3].

Timing with decorator

Decorators are very powerful tools in Python since it allows programmers to modify the behavior of a function, method or even a class. Decorators wrap another function in order to extend the behavior of the wrapped function, without permanently modifying it [ref 4].

def timeit(func):
    ''' Decorator for timing execution of methods'''

    def wrapper(*args, **kwargs):
        start = time.time()
        func(*args, **kwargs)
        duration = '{:.3f}'.format(time.time() - start)
        logging.info(f'{args[1]}:{args[3]}\t{duration} secs.')
        return 0

    return wrapper


Benchmark implementation

The objective is to automate the comparison of the various framework and functions by creating a wrapper EvalFunction class.
The evaluation class has two arguments:
  • Descriptive name of the function, func_name used to evaluate the data structures
  • The signature of the function , func used to evaluate the data structures
import array as ar
import time
import numpy as np
from random import Random
from typing import List, AnyStr, Callable, Any, NoReturn
import math
import torch
from dataclasses import dataclass
import logging
from matplotlib import pyplot as plt



collector = {}


@dataclass
class EvalFunction:
    """
     Data class for evaluation of Python lists, Array, Numpy array and torch tensor
     :param func_name Description of the function to execute
     :param func Lambda to be executed
    """
   func_name: AnyStr
   func: Callable[[Any], float]

   
   def compare(self, input_list: List[float], fraction: float = 0.0) -> NoReturn:
       input_max: int = \
               math.floor(len(input_list)*fraction) if 0.0 < fraction <= 1.0 \
               else len(input_list)

       input_data = input_list[:input_max]

       # Execute lambda through Python list
       self.__execute('python', input_data, 'list:      ')

       # Execute lambda through Python array
       input_array = ar.array('d', input_data)
       self.__execute('python', input_array, 'array:      ')

       # Execute lambda through numpy array
       np_input = np.array(input_list, dtype=np.float32)
       self.__execute('python', np_input, 'lambda: ')

       # Execute native numpy methods
       self.__execute('numpy', np_input, 'native:   ')

       # Execute PyTorch method on CPU
       tensor = torch.tensor(np_input, dtype=torch.float32, device='cpu')
       self.__execute('pytorch', tensor, '(CPU):    ')

       # Execute PyTorch method on GPU
       tensor = torch.tensor(np_input, dtype=torch.float32, device='cuda:0')
       self.__execute('pytorch', tensor, '(CUDA)')


The implementation of the supporting, private method, __execute is described in the Appendix

Evaluation

We've chosen a collection of mathematical transformations that vary in complexity and computational demand to evaluate different frameworks. These transformations involve calculating the mean values produced by the subsequent functions:
\[x_{i}=1+rand{[0, 1]}\]
\[average(x)=\frac{1}{n}\sum_{1}^{n}x_{i}\]
\[sine(x) = average\left ( \sum_{1}^{n}sin\left ( x_{i} \right ) \right )\]
\[sin.exp(x) = average\left ( \sum_{1}^{n}sin\left ( x_{i} \right ) e^{-x_{i}^{2}} \right )\]
\[sin.exp.log(x) = average\left ( \sum_{1}^{n}sin\left ( x_{i} \right ) e^{-x_{i}^{2}} + log(1 + x_{i}))\right )\]

# Functions to evaluate data structures
def average(x) -> float:
    return sum(x)/len(x)
def sine(x) -> float:
    return sum([math.sin(t) for t in x])/len(x)
def sin_exp(x) -> float:
    return sum([math.sin(t)*math.exp(-t) for t in x])/len(x)


# Random value generator
rand = Random(42)
num_values = 500_000_000
my_list: List[float] = [1.0 + rand.uniform(0.0, 0.1)] * num_values

# Fraction of the original data set of 500 million data points
fractions = [0.2, 0.4, 0.6, 0.8, 1.0]



# Evaluate the latency for sub data sets of size , len(my_list)*fraction
for fraction in fractions:
    eval_average = EvalFunction('sin_exp', average)
    eval_average.compare(my_list, fraction)

# x-axis values as size=  len(my_list)*fraction
data_sizes = [math.floor(num_values*fraction) for fraction in fractions]

# Invoke the plotting method
plotter = Plotter(data_sizes, collector)
plotter.plot('Sin*exp 500M')

We conducted the test on an AWS EC2 instance of type p3.2xlarge, equipped with 8 virtual cores, 64GB of memory, and an Nvidia V100 GPU. A basic method for plotting the results is provided in the appendix.

Study 1
We compared the computation time required to determine the {x} -> average{x}  of 500 million real numbers within a Python list, array, NumPy array, and PyTorch tensor.


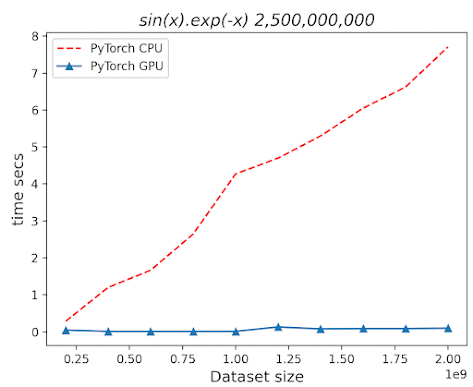
We compared the computation time required to apply the {x} -> sin{x}.exp{-x} function to 500 million real numbers within a Python list, array, NumPy array, and PyTorch tensor.


Conclusion
  • The performance difference between executing on the GPU versus the CPU becomes more pronounced as the dataset size grows.
  • Predictably, the runtime for both the 'average' and 'sin_exp' functions scales linearly with the size of the dataset when using Python lists or arrays.
  • When executed on the CPU, PyTorch tensors show a 20% performance improvement over NumPy arrays.

Study 2
Le't compare the relative performance of GPU and GPU during the processing of a large PyTorch tensor.


Conclusion
The size of dataset has a very limited impact on the performance of processing PyTorch tensor on GPU while the execution time increases linearly on CPU.

Thank you for reading this article. For more information ...

References


Appendix

The __execute method take two arguments used in the structural pattern match:
  • The framework used to identify the
  • The input data to be processed
The private method __numpy_func applies each the functions (average, sine,...) to a NumPy array, np_array generated from the original list.
The method, __pytorch_func applies each function to a torch tensor derived from np_array.


def __execute(self, framework: AnyStr, input: Any) -> float:
    match framework:
        case 'python':
           return self.func(input)
        case 'numpy':
           return self.__numpy_func(input)
        case 'pytorch':
           return self.__pytorch_func(input)
        case _
           return -1.0


def __numpy_func(self, np_array: np.array) -> float:
   match self.func_name:
      case 'average':
          return np.average(np_array).item()
      case 'sine':
          return np.average(np.sin(np_array)).item()
      case 'sin_exp':
          return np.average(np.sin(np_array)*np.exp(-np_array)).item()


def __pytorch_func(self, tensor: torch.tensor) -> float:
    match self.func_name:
       case 'average':
          return torch.mean(tensor).float()
       case 'sine':
          return torch.mean(torch.sin(tensor)).float()
       case 'sin_exp':
          return torch.mean(torch.sin(tensor) * torch.exp(-tensor)).float()


A simple class, Plotter, to wraps the creation and display of plots using matplotlib.

class Plotter(object):
    markers = ['r--', '^-', '+--', '--', '*-']

    def __init__(self, dataset_sizes: List[int], results_map):
        self.sizes = dataset_sizes
        self.results_map = results_map

    def plot(self, title: AnyStr) -> NoReturn:
        index = 0
        np_sizes = np.array(self.sizes)
        for key, values in self.results_map.items():
            np_values = np.array(values)
            plt.plot(np_sizes, np_values, Plotter.markers[index % len(Plotter.markers)])
            index += 1

        plt.title(title, fontsize=16, fontstyle='italic')
        plt.xlabel('Dataset size', fontsize=13, fontstyle='normal')
        plt.ylabel('time secs', fontsize=13, fontstyle='normal')
        plt.legend(['Python List', 'Python Array', 'Numpy native', 'PyTorch CPU', 'PyTorch GPU'])
        plt.show()


---------------------------
Patrick Nicolas has over 25 years of experience in software and data engineering, architecture design and end-to-end deployment and support with extensive knowledge in machine learning. 
He has been director of data engineering at Aideo Technologies since 2017 and he is the author of "Scala for Machine Learning" Packt Publishing ISBN 978-1-78712-238-3

Posted by
Labels: , , , , , ,

No comments:

Post a Comment

Note: Only a member of this blog may post a comment.

Subscribe to: Post Comments (Atom)